(%i1) /* Following "Hydrodynamics II" by Dr. Dullemond at http://www.mpia.de/homes/dullemon/lectures/fluiddynamics/ */"";

Result

(%i2) /* eigenvector helper functions. TODO put these elsewhere, in a file of their own */"";

Result

(%i3) /* maxima returns two lists: one of unique eigenvalues and one of multiplicity.
this duplicates those entries to create a correct list to pass to a diagonal matrix */
eigenvalueList(eigenvectorResults) := flatten(makelist(makelist(eigenvectorResults[1][1][i],eigenvectorResults[1][2][i]), i, 1, length(eigenvectorResults[1][1])));

Result

(%i4) eigenvalueMatrix(eigenvectorResults) := diag(eigenvalueList(eigenvectorResults));

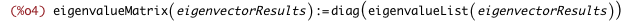
Result

(%i5) /* ... and this takes the 2nd element, containing the eigenvectors and their associated eigenvalues, grouped by eigenvalue multiplicity,
and returns a list of vectors that runs parallel to the eigenvalueList function */
eigenvectorList(eigenvectorResults) := apply(append, eigenvectorResults[2]);

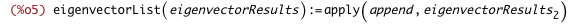
Result

(%i6) eigenvectorMatrix(eigenvectorResults) :=
    block([el,n],
        el : eigenvectorList(eigenvectorResults),
        n : length(el),
        genmatrix(lambda([i,j], el[j][i]), n,n)
    );

Result

(%i7) /* convince diff to not treat variables as constants */ depends(P, %rho);

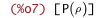
Result

(%i8) /* density = particle number density times mean weight of gas particle */ %rho_from_N_%mu : %rho = N * %mu;

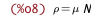
Result

(%i9) N_from_%rho_%mu : solve(%rho_from_N_%mu, N)[1];

Result

(%i10) /* specific energy - kinetic, internal, and total */"";

Result

(%i11) /* internal energy = density times internal specific energy */ E = %rho * e;

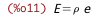
Result

(%i12) v : [vx, vy, vz];

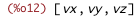
Result

(%i13) /* fluid velocity */ vLenSq_from_v : vLen^2 = v.v;

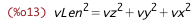
Result

(%i14) v_from_vLenSq : rhs(vLenSq_from_v) = lhs(vLenSq_from_v);

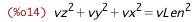
Result

(%i15) /* specific kinetic energy */
eKin_from_vLen : eKin = vLen^2/2;

Result

(%i16) eKin_from_v : subst([vLenSq_from_v], eKin_from_vLen);

Result

(%i17) eTotal_from_eKin_e : eTotal = eKin + e;

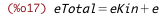
Result

(%i18) e_from_eTotal_eKin : solve(eTotal_from_eKin_e, e)[1];

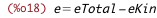
Result

(%i19) /* Pressure */"";

Result

(%i20) /* ideal gas law */ P_from_N_k_T : P = N * k * T;

Result

(%i21) P_from_k_T_%rho_%mu : P_from_N_k_T, N_from_%rho_%mu;

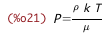
Result

(%i22) /* another ideal gas law property */ P_from_%rho_e : P = (%gamma - 1) * %rho * e;

Result

(%i23) e_from_P_%rho : solve(P_from_%rho_e, e)[1];

Result

(%i24) eTotal_from_eKin_%rho_P : subst([e_from_P_%rho], eTotal_from_eKin_e);

Result

(%i25) P_from_%rho_eTotal_vLen : subst([e_from_eTotal_eKin, eKin_from_vLen], P_from_%rho_e);

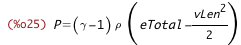
Result

(%i26) P_from_%rho_eTotal_v : subst([vLenSq_from_v], P_from_%rho_eTotal_vLen);

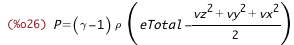
Result

(%i27) eTotal_from_%rho_v_P : subst([eKin_from_v], eTotal_from_eKin_%rho_P);

Result

(%i28) /* internal specific enthalpy */"";

Result

(%i29) h_from_e_P_%rho : h = e + P / %rho;

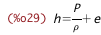
Result

(%i30) h_from_P_%rho : ratsimp(subst([e_from_P_%rho], h_from_e_P_%rho));

Result

(%i31) h_from_e : ratsimp(subst([P_from_%rho_e], h_from_e_P_%rho));

Result

(%i32) /* total specific enthalpy */"";

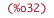
Result

(%i33) hTotal_from_h_eKin : hTotal = h + eKin;

Result

(%i34) h_from_hTotal_eKin : solve(hTotal_from_h_eKin, h)[1];

Result

(%i35) hTotal_from_eTotal_P_%rho : hTotal = P / %rho + eTotal;

Result

(%i36) hTotal_from_P_%rho : subst([eTotal_from_eKin_%rho_P], hTotal_from_eTotal_P_%rho);

Result

(%i37) /* speed of sound */"";

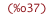
Result

(%i38) assume(Cs > 0);

Result

(%i39) /* adiabatic compression/expansion */
P_from_K_%rho_%gamma : P = K * %rho ^ %gamma;

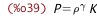
Result

(%i40) K_%rho_%gamma_from_P : rhs(P_from_K_%rho_%gamma) = lhs(P_from_K_%rho_%gamma);

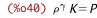
Result

(%i41) /* adiabatic sound speed: Cs^2 = dP/d%rho */
CsSq_from_K_%rho_%gamma : Cs^2 = diff(subst(P_from_K_%rho_%gamma, P), %rho);

Result

(%i42) /* ...in terms of pressure */
CsSq_from_P_%rho : lhs(CsSq_from_K_%rho_%gamma) = rhs(CsSq_from_K_%rho_%gamma) * lhs(P_from_K_%rho_%gamma) / rhs(P_from_K_%rho_%gamma);

Result

(%i43) CsSq_from_P_%rho / %gamma$
rhs(%) = lhs(%)$
P_%rho_from_CsSq : %;

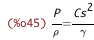
Result

(%i46) P_from_%rho_CsSq : P_%rho_from_CsSq * %rho;

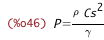
Result

(%i47) /* in terms of specific internal energy */
CsSq_from_e : lhs(CsSq_from_P_%rho) = rhs(CsSq_from_P_%rho) * lhs(e_from_P_%rho) / rhs(e_from_P_%rho);

Result

(%i48) /* in terms of enthalpy */
CsSq_from_h : lhs(CsSq_from_e) = ratsimp(rhs(CsSq_from_e) * lhs(h_from_e) / rhs(h_from_e));

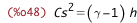
Result

(%i49) /* isothermal sound speed ... not used */
csSq_from_e : cs^2 = (%gamma - 1) * e;

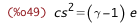
Result

(%i50) h_from_hTotal_vLen : subst([eKin_from_vLen], solve(hTotal_from_h_eKin, h)[1]);

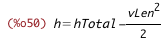
Result

(%i51) CsSq_from_hTotal : subst([h_from_hTotal_vLen], CsSq_from_h);

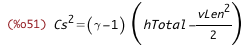
Result

(%i52) hTotal_from_CsSq_vLen : solve(CsSq_from_hTotal, hTotal)[1];

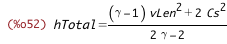
Result

(%i53) hTotal_from_CsSq_v : subst([vLenSq_from_v], hTotal_from_CsSq_vLen);

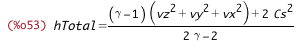
Result

(%i54) CsSq_from_eTotal_vLen : subst([e_from_eTotal_eKin, eKin_from_vLen], CsSq_from_e);

Result

(%i55) /* take the positive root */ Cs_from_eTotal_vLen : solve(CsSq_from_eTotal_vLen, Cs)[2];

Result

(%i56) eTotal_v_from_Cs : subst([vLenSq_from_v], rhs(Cs_from_eTotal_vLen) = lhs(Cs_from_eTotal_vLen));

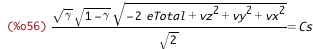
Result

(%i57) /* Euler equations of motion */"";

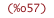
Result

(%i58) xs : [x,y,z];

Result

(%i59) primitives : append([%rho], v, [eTotal]);

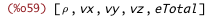
Result

(%i60) states : [q1, q2, q3, q4, q5];

Result

(%i61) depends(append(primitives, states, [P]), append([t],xs));

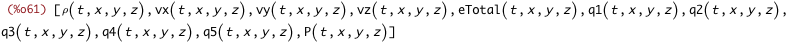
Result

(%i62) /* equations, separate */"";

Result

(%i63) primitive_eqn_density : 'diff(%rho, t) + sum('diff(%rho * v[i], xs[i]),i,1,3) = 0;

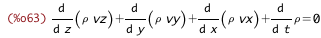
Result

(%i64) primitive_eqn_velocity : create_list('diff(%rho * v[j], t) + sum('diff(%rho * v[j] * v[i] + kron_delta(j,i)*P, xs[i]), i,1,3) = 0, j, [1,2,3]);

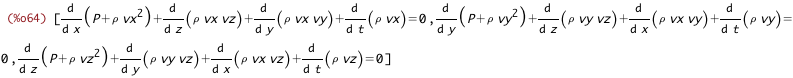
Result

(%i65) primitive_eqn_energy : 'diff(%rho * eTotal, t) + sum('diff(v[i] * (%rho * eTotal + P), xs[i]),i,1,3) = 0;

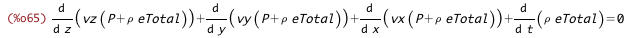
Result

(%i66) /* Euler equations using primitive variables */
append([primitive_eqn_density], primitive_eqn_velocity, [primitive_eqn_energy])$
subst([P_from_%rho_eTotal_v, vLenSq_from_v], %)$
primitive_eqns : %;

Result

(%i69) /* state variables in terms of primitive variables */
states_from_primitives : [q1 = %rho, q2 = %rho * vx, q3 = %rho * vy, q4 = %rho * vz, q5 = %rho * eTotal];

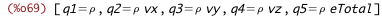
Result

(%i70) /* primitive variables from state variables */ primitives_from_states : solve(states_from_primitives, primitives)[1];

Result

(%i71) state_eqns : subst(primitives_from_states, primitive_eqns);

Result

(%i72) dt_from_state_eqns : create_list(lhs(state_eqns[i]) - 'diff(states[i],t) = rhs(state_eqns[i]) -'diff(states[i],t),i,[1,2,3,4,5]);

Result

(%i73) dt_from_state_eqns_lhs : create_list(lhs(eqn), eqn, dt_from_state_eqns);

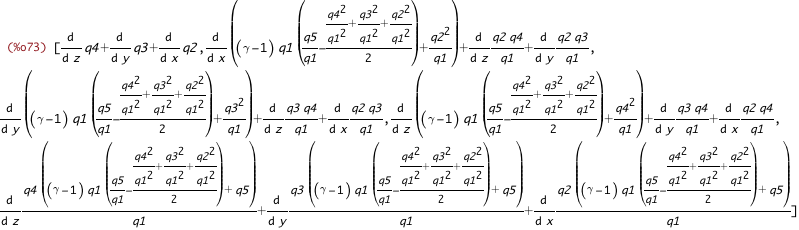
Result

(%i74) dt_from_state_eqns_rhs : create_list(rhs(eqn), eqn, dt_from_state_eqns);

Result

(%i75) state_eqns_from_dt_matrix : genmatrix(lambda([i,j], dt_from_state_eqns_lhs[i]),5,1) = genmatrix(lambda([i,j], dt_from_state_eqns_rhs[i]),5,1);

Result

(%i76) state_eqns_from_dt_matrix_ev : expand(ev(state_eqns_from_dt_matrix, diff));

Result

(%i77) state_eqns_diffx_jacobian : genmatrix(lambda([i,j], ratsimp(coeff(lhs(state_eqns_from_dt_matrix_ev)[i,1], diff(states[j],x)))), 5, 5);

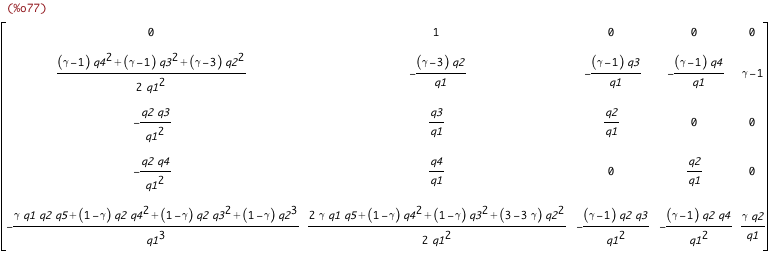
Result

(%i78) primitive_eqns_diffx_jacobian : ratsimp(subst(states_from_primitives, state_eqns_diffx_jacobian));

Result

(%i79) /* would be great if I could declare a matrix multiply without it expanding...
so I could show the original equation with the state vector derivative factored out */
state_eqns_diffx_jacobian . genmatrix(lambda([i,j], diff(states[i],x)), 5, 1) = rhs(state_eqns_from_dt_matrix_ev);

Result

(%i80) /* now to find the eigenvalues and eigenvectors of the state_eqn matrix */"";

Result

(%i81) diffx_jacobian_eigenvector_results : eigenvectors(primitive_eqns_diffx_jacobian);

Result

(%i82) eigenvalueList(diffx_jacobian_eigenvector_results)$
create_list(subst(eTotal_v_from_Cs, expand(eqn)), eqn, %)$
diffx_jacobian_eigenvalues : %;

Result

(%i85) load(diag);

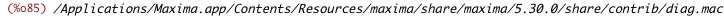
Result

(%i86) diffx_jacobian_eigenvalue_matrix : diag(diffx_jacobian_eigenvalues);

Result

(%i87) eigenvectorList(diffx_jacobian_eigenvector_results)$
% : expand(%)$
genmatrix(lambda([i,j], subst([eTotal_v_from_Cs], %[j][i])), 5, 5)$
/* now that Maxima has put a "v" in the middle of the components that make up Cs,
there is no way to move the "v" to the left side of the multiplication,
and there is no way to substitute in the Cs. HAVE TO DO IT BY HAND, THANK YOU MAXIMA.
TODO: find a way to rearrange elements of a product ... or just split a sum or product into a list. */
% : subst([sqrt(%gamma) * sqrt(1-%gamma) * vx * sqrt(vx^2+vy^2+vz^2-2*eTotal)/sqrt(2) = vx*Cs], %)$
% : subst([%gamma*eTotal - %gamma*vz^2/2 + vz^2/2 - %gamma*vy^2/2 + vy^2/2 - %gamma*vx^2/2 + vx^2/2 - Cs*vx = hTotal - Cs*vx], %)$
% : subst([%gamma*eTotal - %gamma*vz^2/2 + vz^2/2 - %gamma*vy^2/2 + vy^2/2 - %gamma*vx^2/2 + vx^2/2 + Cs*vx = hTotal + Cs*vx], %)$
diffx_jacobian_eigenvectors : %;

Result

(%i94) ratsimp(invert(diffx_jacobian_eigenvectors))$
ratsimp(subst([hTotal_from_CsSq_v], %))$
diffx_jacobian_eigenvectors_inverse : %;

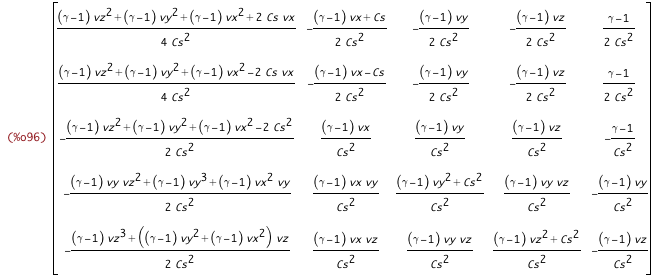
Result

(%i97) /* could go for one last vSq substitution ... */"";

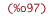
Result

(%i98) /* verify that the eigenvector and eigenvector inverse matrices are inverses */
diffx_jacobian_eigenvectors . diffx_jacobian_eigenvectors_inverse$
subst([hTotal_from_CsSq_v], %)$
ratsimp(%);
is(equal(%, ident(5)));

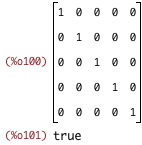
Result

(%i102) /* verify that the eigenvectors reconstruct to the original matrix */
diffx_jacobian_eigenvectors . diffx_jacobian_eigenvalue_matrix . diffx_jacobian_eigenvectors_inverse$
subst([hTotal_from_CsSq_v], %)$
ratsimp(%)$
subst([CsSq_from_eTotal_vLen, vLenSq_from_v], %)$
ratsimp(%);
is(equal(%, primitive_eqns_diffx_jacobian));
primitive_eqns_diffx_jacobian;

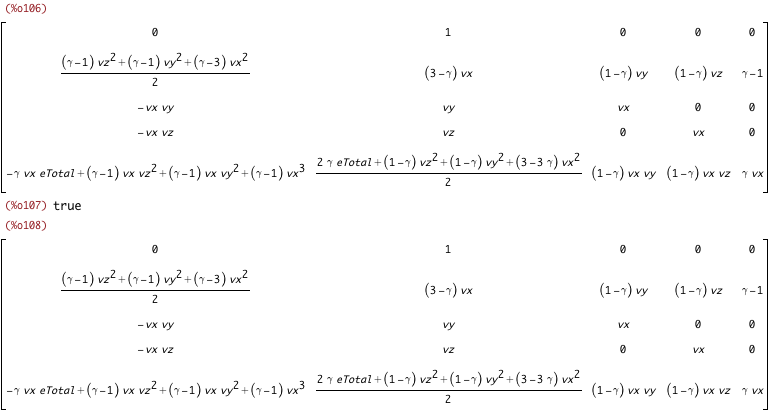
Result

(%i109) /* verify that the eigenvectors do scale by the eigenvalue */"";
for i : 1 thru 5 do (
    block([x],
        x : col(diffx_jacobian_eigenvectors, i),
        x : primitive_eqns_diffx_jacobian . x = diffx_jacobian_eigenvalues[i] * x,
        x : subst([hTotal_from_CsSq_v], x),
        x : ratsimp(x),
        x : subst([eTotal_from_eKin_e, eKin_from_vLen, vLenSq_from_v, solve(CsSq_from_e, e)[1]], x),
        x : ratsimp(x),
        print(x),
        print(is(equal(lhs(x), rhs(x))))
));

Result

(%i111) /* verify that the eigenvectors do scale by the eigenvalue */"";
for i : 1 thru 5 do (
    block([x],
        x : row(diffx_jacobian_eigenvectors_inverse, i),
        x : x . primitive_eqns_diffx_jacobian = diffx_jacobian_eigenvalues[i] * x,
        x : subst([hTotal_from_CsSq_v], x),
        x : ratsimp(x),
        x : subst([eTotal_from_eKin_e, eKin_from_vLen, vLenSq_from_v, solve(CsSq_from_e, e)[1]], x),
        x : ratsimp(x),
        print(x),
        print(is(equal(lhs(x), rhs(x))))
));

Result

(%i113) /* rather than solving the derivative of the flux with regards to the conservative variables directly,
more advanced systems solve the derivative of the flux with regards to the primitive variables
and then the derivative of the conservatives with regards to the primitives
(like Trangenstein, J.) */"";

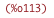
Result

(%i114) primitives2 : append([%rho], v, [P]);

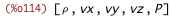
Result

(%i115) subst(append(states_from_primitives, [eTotal_from_%rho_v_P]), states)$
expand(%)$
states_from_primitives2 : %;

Result

(%i118) jacobian(states_from_primitives2, primitives2)$
ratsimp(%)$
diff_state_wrt_primitives2 : %;

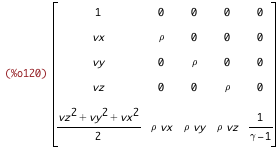
Result

(%i121) diff_primitives2_wrt_state : invert(diff_state_wrt_primitives2);

Result

(%i122) primitive_eqns$
subst([eTotal_from_%rho_v_P], %)$
create_list(lhs(%[i]), i, [1,2,3,4,5])$
expand(ev(%, diff))$
genmatrix(lambda([i,j], ratsimp(coeff(lhs(%)[i], diff(primitives2[j],x)))), 5, 5)$
diff_flux_wrt_primitives2 : %;

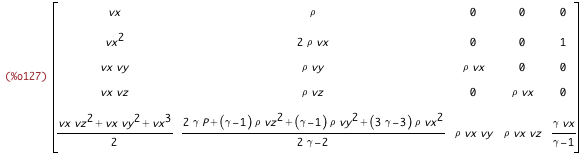
Result

(%i128) /* verify dF/du = dF/dw (du/dw)^-1 */
diff_flux_wrt_primitives2 . diff_primitives2_wrt_state$
subst([P_from_%rho_eTotal_v], %)$
ratsimp(%);
is(equal(%, primitive_eqns_diffx_jacobian));
primitive_eqns_diffx_jacobian;

Result

(%i133) /* Trangenstein calculates (du/dw)^-1 dF/dw ...
and subtracts out the diagonal to get the Acoustic matrix */
diff_primitives2_wrt_state . diff_flux_wrt_primitives2$
ratsimp(%)$
Acoustic_plus_velocity : %;

Result

(%i136) Acoustic : Acoustic_plus_velocity - ident(5) * vx;

Result

(%i137) Acoustic_eigenvector_results : eigenvectors(Acoustic);

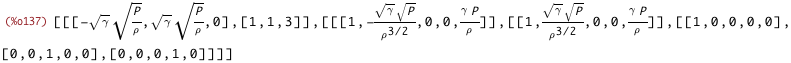
Result

(%i138) eigenvalueList(Acoustic_eigenvector_results)$
subst([P_%rho_from_CsSq], %)$
diag(%)$
Acoustic_eigenvalue_matrix : %;

Result

(%i142) eigenvectorMatrix(Acoustic_eigenvector_results)$
subst([P_from_%rho_CsSq], %)$
% * %rho$
Acoustic_eigenvector_matrix : %;

Result

(%i146) invert(Acoustic_eigenvector_matrix)$
Acoustic_eigenvector_inverse_matrix : %;

Result

(%i148) /* now the acoustic eigenvector matrix times the jacobian of primitives wrt states should be the flux eigenvector matrix */
jacobian_state_wrt_primtives2 . Acoustic_eigenvector_matrix;

Result

Created with wxMaxima.